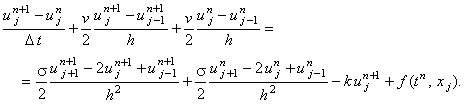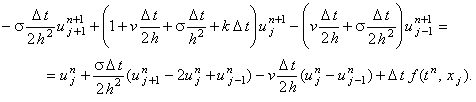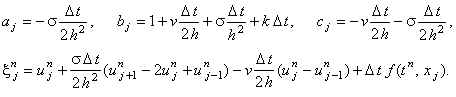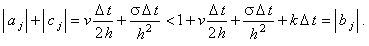При описании методов решения дифференциальных уравнений параболического типа, не содержащих производную по координате первого порядка, рассматривалась разностная схема Кранка-Николсона, обладающая абсолютной устойчивостью и вторым порядком аппроксимации по времени (в отличие от явной и неявной разностных схем). Запишем разностную схему Кранка-Николсона для уравнения (6.1):

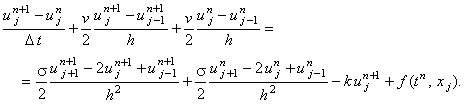(6.7)

Обратим внимание, что для сохранения второго порядка аппроксимации по времени производную по координате первого порядка необходимо представить также, как и производную по координате второго порядка, т.е. в виде суммы двух слагаемых, одно из которых аппроксимируется на (n + 1)-ом шаге по времени, а другое - на n-ом шаге по времени.
     Разностная схема (6.7) является абсолютно устойчивой (доказательство в силу сложности не приводится) и имеет порядок аппроксимации:
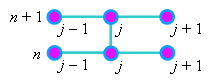
     Разностный шаблон (см. рисунок), характеризующий разностную схему (6.7), свидетельствует о том, что она содержит три неизвестные величины - значения функции u на (n + 1)-ом шаге по времени. Следовательно, для её решения необходимо использовать метод прогонки.
     Приведём разностную схему (6.7) к виду (4.10), удобному для использования метода прогонки: Следовательно, коэффициенты, соответствующие уравнению (4.10), имеют вид: Легко видеть, что для разностной схемы (6.7) достаточное условие сходимости прогонки (4.16) выполняется:      Алгоритм решения, а также методики определения прогоночных коэффициентов и решения на правой границе аналогичны описанным ранее.