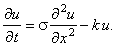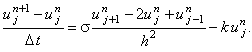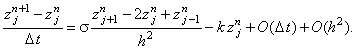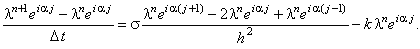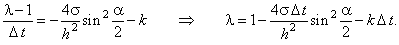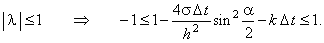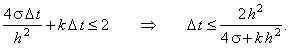|
Рассмотрим одномерное дифференциальное уравнение параболического типа,
свободный член которого включает искомую функцию u следующим образом:
| |
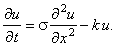 |
(3.13) |
Подобные уравнения часто встречаются в математических моделях химических реакторов, в которых
протекают прямые реакции. Поэтому важно знать, каким образом наличие подобного свободного члена
влияет на устойчивость разностных схем.
Запишем для уравнения (3.13) явную разностную схему:
| |
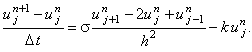 |
(3.14) |
Осуществляя выкладки, аналогичные описанным ранее (для случая уравнения, свободный член которого
не включает функцию u), можно получить разностную схему для погрешности решения, которая будет
иметь вид:
Наличие слагаемого 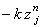 в правой части данного уравнения говорит о том, что свободный член в
уравнении (3.13) влияет на погрешность вычислений, поэтому отбрасывать его при анализе устойчивости разностной схемы (3.14) нельзя. в правой части данного уравнения говорит о том, что свободный член в
уравнении (3.13) влияет на погрешность вычислений, поэтому отбрасывать его при анализе устойчивости разностной схемы (3.14) нельзя.
Представляя решение разностной схемы (3.14) в виде гармоники (3.7), получаем:
Далее, деля левую и правую части данного выражения на 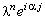 и используя зависимости (3.9), (3.10),
получаем формулу, из которой затем выражаем и используя зависимости (3.9), (3.10),
получаем формулу, из которой затем выражаем  :
С учётом необходимого условия устойчивости разностных схем (3.8) имеем:
Анализ полученного неравенства, аналогичный описанному выше
(для случая уравнения, свободный член которого не включает функцию u), позволяет получить
условие устойчивости явной разностной схемы (3.14), аппроксимирующей уравнение (3.13): :
С учётом необходимого условия устойчивости разностных схем (3.8) имеем:
Анализ полученного неравенства, аналогичный описанному выше
(для случая уравнения, свободный член которого не включает функцию u), позволяет получить
условие устойчивости явной разностной схемы (3.14), аппроксимирующей уравнение (3.13):
Легко доказать, что на абсолютную устойчивость неявной разностной схемы, аппроксимирующей уравнение (3.13),
наличие рассматриваемого свободного члена не повлияет.
|
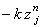 в правой части данного уравнения говорит о том, что свободный член в
уравнении (3.13) влияет на погрешность вычислений, поэтому отбрасывать его при анализе устойчивости разностной схемы (3.14) нельзя.
в правой части данного уравнения говорит о том, что свободный член в
уравнении (3.13) влияет на погрешность вычислений, поэтому отбрасывать его при анализе устойчивости разностной схемы (3.14) нельзя.
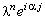 и используя зависимости (3.9), (3.10),
получаем формулу, из которой затем выражаем
и используя зависимости (3.9), (3.10),
получаем формулу, из которой затем выражаем  :
: