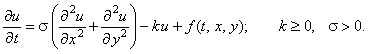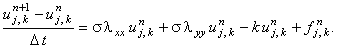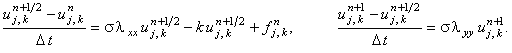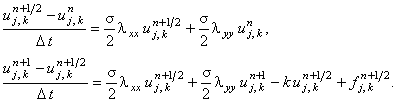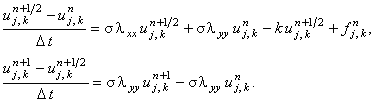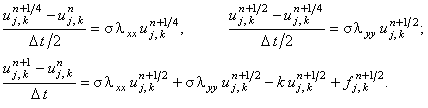Решение двумерных дифференциальных уравнений параболического типа.
       10. Сравнительная характеристика изученных разностных схем.

     В заключение приведём сравнительную характеристику разностных схем, аппроксимирующих двумерное дифференциальное уравнение параболического типа, не содержащее первых производных по координатам x и y:
 
При записи разностных схем использованы обозначения (7.6).

     1. Явная разностная схема
 

  • Имеет порядок аппроксимации
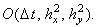  • Условно устойчива
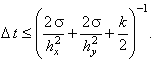  • Решается с помощью рекуррентного соотношения (7.5).

         2. Схема расщепления
     
  • Имеет порядок аппроксимации
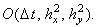  • Абсолютно устойчива.
  • Каждая подсхема решается с помощью метода прогонки.

         3. Схема переменных направлений
     
  • Имеет порядок аппроксимации
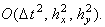  • Абсолютно устойчива.
  • Каждая подсхема решается с помощью метода прогонки.

         4. Схема со стабилизирующей поправкой
     
  • Имеет порядок аппроксимации
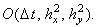  • Абсолютно устойчива.
  • Каждая подсхема решается с помощью метода прогонки.

         5. Схема предиктор-корректор
     
  • Имеет порядок аппроксимации
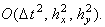  • Абсолютно устойчива.
  • Каждая из подсхем предиктора решается с помощью метода прогонки; корректор (третья подсхема) - с помощью рекуррентного соотношения (7.18).